When to Mark visited: BFS, DFS, and Dijkstra Explained Precisely
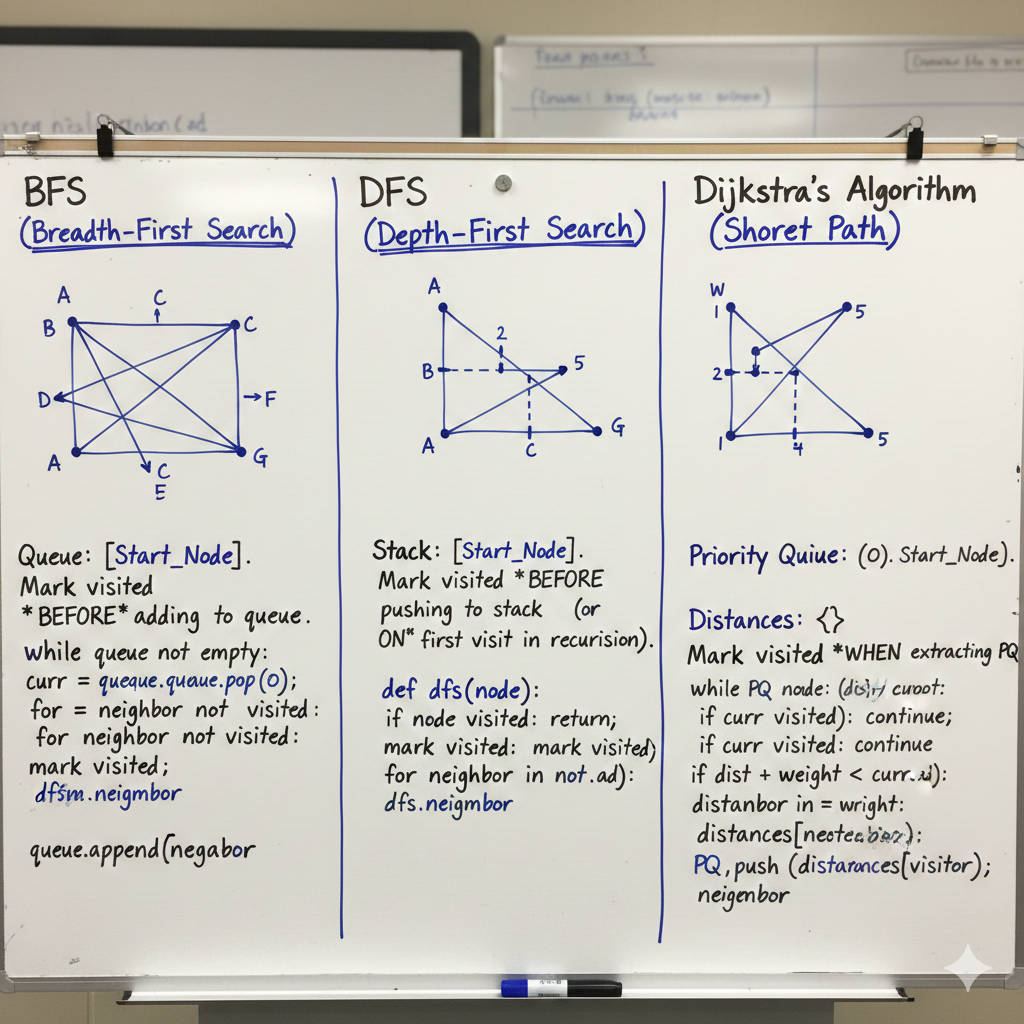
Abstract
One of the most common sources of bugs in graph algorithms is marking a node as visited at the wrong time. This article explains exactly when and why nodes must be marked visited in BFS, DFS, and Dijkstra, based on their formal correctness invariants—not intuition or convention.
The Core Idea
The timing of visited is not an implementation detail. It encodes what property of the node has become irreversible.
A node must be marked
visitedat the moment the algorithm’s guarantee becomes final.
Each algorithm has a different guarantee. Therefore, each marks visited at a different time.
BFS (Breadth-First Search)
What visited Means
Visited = discovered
Once a node is discovered in BFS, the shortest path (in number of edges) to that node is already known.
Why This Works
- All edges have equal weight
- BFS explores level by level
- The first time a node is reached is optimal
Correct Invariant
A node must enter the queue at most once.
Correct Timing
Mark visited when enqueuing, not when dequeuing.
Correct Pattern
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)What Breaks if You Mark Late
- Duplicate enqueues
- Redundant processing
- Potential exponential blowup in dense graphs
DFS (Depth-First Search)
What visited Means
Visited = entered
Once DFS enters a node, re-entering it provides no new information and creates cycles.
Why This Works
- DFS is about coverage, not optimality
- Cycles must be prevented immediately
Correct Invariant
A node must never be entered more than once along the active call stack.
Correct Timing
Mark visited when entering the node (before recursion).
Correct Recursive Pattern
def dfs(node):
visited.add(node)
for n in node.neighbors:
if n not in visited:
What Breaks if You Mark Late
- Infinite recursion in cyclic graphs
- Exponential revisits in DAGs
Dijkstra’s Algorithm
What visited Means
Visited = distance finalized
A node may be discovered multiple times with improving distances. visited means no further improvement is possible.
Why Early Marking Is Wrong
- Edge weights vary
- First discovery is not necessarily optimal
- A later path may be cheaper
Correct Invariant
When a node is extracted as the global minimum from the priority queue, its shortest distance is final.
Correct Timing
Mark visited when the node is popped from the priority queue.
Correct Pattern
while pq:
dist, u = heappop(pq)
if u in visited:
continue
visited.add(u)
for vWhat Breaks if You Mark Early
Incorrect shortest paths.
Example:
A --10--> B
A --1--> C --1--> B
Early marking fixes B at distance 10 and blocks the optimal path of 2.
Comparison Table
| Algorithm | Edge Weights | Meaning of visited | When to Mark |
|---|---|---|---|
| BFS | Equal | Discovered | Enqueue |
| DFS | Irrelevant | Entered | Entry / Push |
| Dijkstra | Non-negative | Distance finalized | Min-pop |
Unifying Rule
All three algorithms follow the same principle:
Mark a node visited when the algorithm’s correctness guarantee becomes irreversible.
- BFS: irreversible at discovery
- DFS: irreversible at entry
- Dijkstra: irreversible at minimum extraction
Final Insight
If you cannot clearly state what property becomes final when you mark visited, the implementation is likely incorrect.
This is not a stylistic choice.
It is a correctness condition.